数据结构与算法系列 - 02 复杂度分析

发表于 | 更新于: | 分类于 | 本文总阅读量 次

参考：03 | 复杂度分析（上）：如何分析、统计算法的执行效率和资源消耗？

时间复杂度分析

大O复杂度表示法

时间复杂度的全称是渐进时间复杂度，表示代码执行时间随数据规模增长的变化趋势

复杂度分析方法

  1. 只关注循环执行次数最多的一段代码
    1
    2
    3
    4
    5
    6
    7
    8
    int cal(int n) {
      int sum = 0;
      int i = 1;
      for (; i <= n; ++i) {
        sum = sum + i;
      }
      return sum;
    }

其中第 2、3 行代码都是常量级的执行时间，与 n 的大小无关，所以对于复杂度并没有影响。循环执行次数最多的是第 4、5 行代码，所以这块代码要重点分析。这两行代码被执行了 n 次，所以总的时间复杂度就是 O(n)。

  1. 加法法则：总复杂度等于量级最大的那段代码的复杂度
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    int cal(int n) {
       int sum_1 = 0;
       int p = 1;
       for (; p < 100; ++p) {
         sum_1 = sum_1 + p;
       }

       int sum_2 = 0;
       int q = 1;
       for (; q < n; ++q) {
         sum_2 = sum_2 + q;
       }

       int sum_3 = 0;
       int i = 1;
       int j = 1;
       for (; i <= n; ++i) {
         j = 1;
         for (; j <= n; ++j) {
           sum_3 = sum_3 +  i * j;
         }
       }

       return sum_1 + sum_2 + sum_3;
     }

这个代码分为三部分，分别是求 sum_1、sum_2、sum_3。我们可以分别分析每一部分的时间复杂度，然后把它们放到一块儿，再取一个量级最大的作为整段代码的复杂度。
其中sum_1是执行100次得到的结果，是一个常量的执行时间，和n的规模无关，所有复杂度为O(1)
sum_2、sum_3分别为O(n)、O(n²)，T(n)=O(1)+O(n)+O(n²)。我们取其中最大的量级。所以，整段代码的时间复杂度就为 O(n²)

如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么T(n)=T1(n)+T2(n)=max(O(f(n))+O(f(n)))=O(max(f(n),g(n)))

  1. 乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    int cal(int n) {
       int ret = 0;
       int i = 1;
       for (; i < n; ++i) {
         ret = ret + f(i);
       }
     }

     int f(int n) {
      int sum = 0;
      int i = 1;
      for (; i < n; ++i) {
        sum = sum + i;
      }
      return sum;
     }

我们单独看 cal() 函数。假设 f() 只是一个普通的操作，那第 4～6 行的时间复杂度就是，T1(n) = O(n)。但 f() 函数本身不是一个简单的操作，它的时间复杂度是 T2(n) = O(n)，所以，整个 cal() 函数的时间复杂度就是，T(n) = T1(n) T2(n) = O(nn) = O(n²)。

如果 T1(n)=O(f(n))，T2(n)=O(g(n))；那么 T(n)=T1(n)T2(n)=O(f(n))O(g(n))=O(f(n)*g(n))

常见复杂度量级

粗略地分为两类，多项式量级和非多项式量级。其中，非多项式量级只有两个：O(2n) 和 O(n!)。

空间复杂度

全称是渐进空间复杂度。表示算法的存储空间与数据规模之间的增长关系

1
2
3
void print(int n){
  int[] a=new int[n];
}

代码中申请了一个大小为n的int类型数组变量a，，那么空间复杂度就是O(n)。
我们常见的空间复杂度就是 O(1)、O(n)、O(n²)，像 O(logn)、O(nlogn) 这样的对数阶复杂度平时都用不到。

总结

复杂度也叫渐进复杂度，包括时间复杂度和空间复杂度，用来分析算法执行效率与数据规模之间的增长关系，可以粗略地表示，越高阶复杂度的算法，执行效率越低。常见的复杂度并不多，从低阶到高阶有：O(1)、O(logn)、O(n)、O(nlogn)、O(n²)。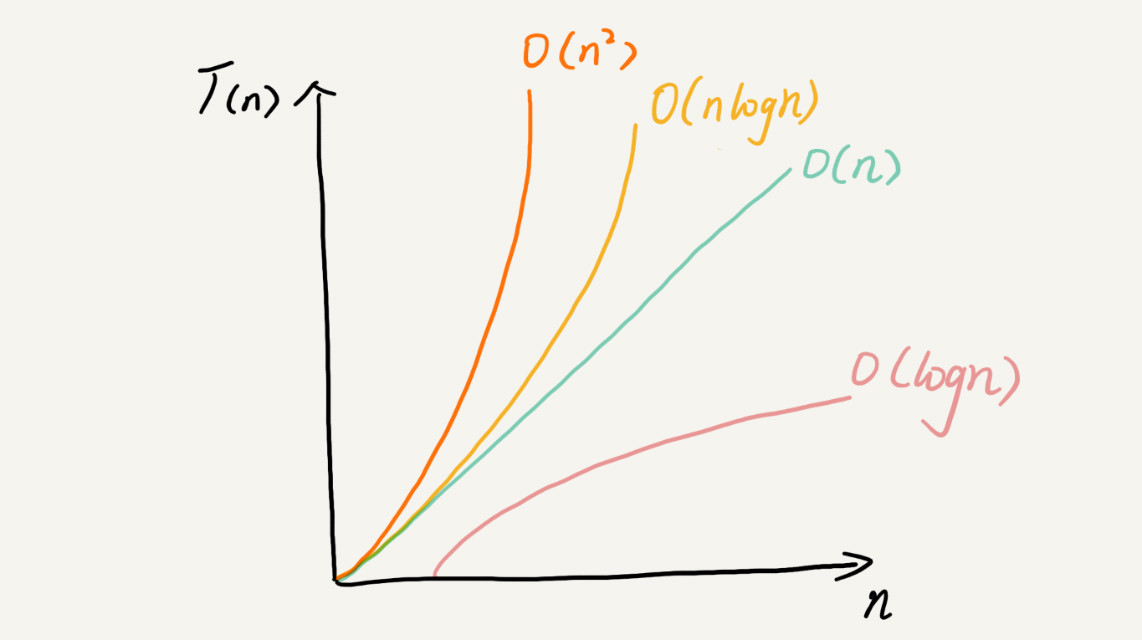

复杂度分析还有4个概念：

  • 最坏情况时间复杂度：代码在最理想情况下执行的时间复杂度。
  • 最好情况时间复杂度：代码在最坏情况下执行的时间复杂度。
  • 平均时间复杂度：用代码在所有情况下执行的次数的加权平均值表示。
  • 均摊时间复杂度：在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。